Ionization potential depression in dense plasmas
The dense plasma state is a common phase of matter in the universe. It can be found in stars and giant planets, and is created during fusion experiments. The electronic structure of an atom embedded in a dense plasma differs significantly from that of an isolated atom.
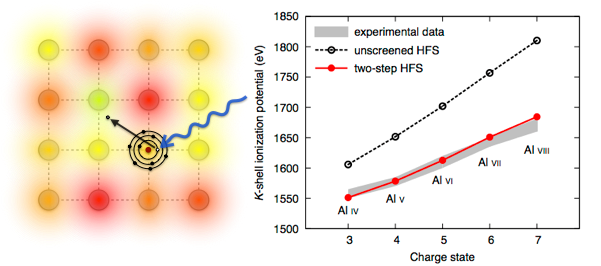
Figure left: Illustration of atoms in a dense plasma and x-ray photoionization process.
Figure right: Ionization potential depression in aluminum plasmas as a function of the charge state.
Due to the screening effect by the charged environment within the plasma, atomic levels shift and the ionization potential becomes reduced in comparison with the isolated atomic case, as shown in Figure. This ionization potential depression (IPD) has so far been described with two distinct theoretical models: Stewart-Pyatt and Ecker-Kröll. However, their validity has recently been disputed by two state-of-the-art experiments, one using an x-ray free-electron laser (LCLS) and the other using a high-power optical laser (Orion). Neither the Stewart-Pyatt model nor the Ecker-Kröll model could explain both experiments. This controversy has profound implications for how to correctly model experiments on dense plasmas.
Here, we present a rigorous and computationally efficient approach to predicting IPDs: a two-step Hartree-Fock-Slater model. Our approach is based on first-principle quantum-mechanical calculations for an atom embedded in a dense plasma, taking into account detailed electronic configurations of plasma ions. In contrast to the Stewart-Pyatt and Ecker-Kröll models, our two-step model successfully describes all available experimental data on IPDs. Calculations within our approach are relatively inexpensive and, therefore, are expected to be applicable for a wide range of plasma conditions---for describing data from studies on warm dense matter, planetary science, and inertial confinement fusion.
Physical Review X 4 (2014) 031004
http://journals.aps.org/prx/abstract/10.1103/PhysRevX.4.031004